证明：如下图，以AB为直径作圆，因为

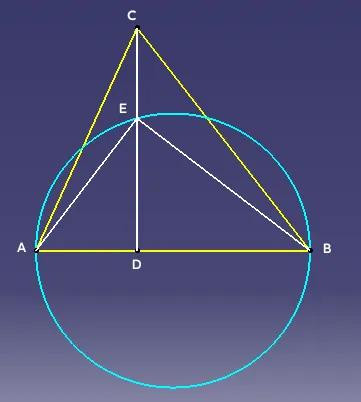
角C为锐角，所以C点必在圆外。过C作CD⊥AB于D，交圆于E，连接AE、BE，由于AB是直径，所以∠AEB=90°。

根据射影定理DE²=AD·DB。又因为tan∠EAD=ED/AD，tan∠EBD=ED/DB，所以tan∠EAD·tan∠EBD=1。

显然tanA=CD/AD＞tan∠EAD，同理可得tanB＞tan∠EBD，所以tanA·tanB＞1

示例二，如下图，AB为圆的直径，C、D为圆上任意两点，连接AD、BD，过C作AB的垂线，垂足为F，交AD于G，交BD延长线于E，则有FC²=FG·FE。

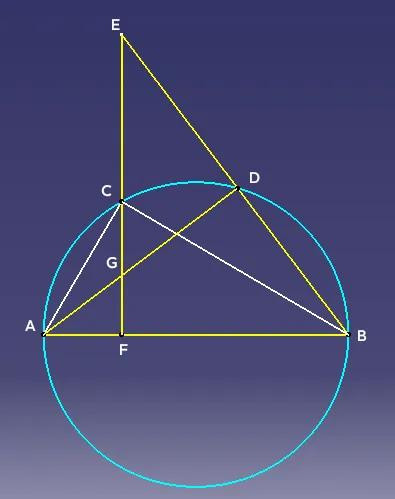
证明：连接CA、CB，则有∠ACB=90°，又CF⊥AB，所以FC²=AF·FB。

同理∠ADB=90°，易得△AGF∽△EBF，所以AF/FG=FE/BF，则AF·FB=FG·FE所以FC²=FG·FE。

以上是C、D在AB同侧的情况，C、D在AB异侧同样成立，有兴趣的可以自行验证。